유니티 스크립트 활용해 절차지향 모델링 기본요소 구성하기
안녕하세요. 어반베이스 3D 그래픽스팀의 윤인하입니다. 어반베이스에서는 비전문가들도 손쉽게 건물 단면도를 모델링 할 수 있는 라이브 스케치(Live Sketch)라는 툴을 개발하고 있습니다.
라이브 스케치를 활용하면, 캐드나 여타 3D모델링 툴(3DsMax, Maya, Blender, SolidWorks, Raino)과는 달리 고도의 학습 없이도 빠르고 쉽게 원하는 건물 단면도를 제작 할 수 있습니다.
라이브 스케치는 기존 모델링 툴에서 제작된 에셋을 가져다가 쓰는 것이 아니라 사용자가 동적으로 모델링을 만들어야 합니다. 물론 일부 심시티 같은 게임은 미리 제작되어 정적으로 보관되어 있는 블럭을 조립하는 식으로 건축물을 제작하기도 하지만, 이런 경우 수정과 편집이 번거롭고 컴퓨터의 연산량도 많아진다는 단점이 있습니다.
그렇기 때문에 일련의 규칙대로 프로그램 런타임에 모델링을 수행할 필요가 있었는데, (소위 절차지향 모델이라고 부릅니다) 이런 절차지향 모델링을 특정 프레임워크에서 수행하기 위해서는 opengl, direct 와 같은 graphic library 에서의 랜더링 기본 구성요소는 물론 구현방식을 우선적으로 알 필요가 있습니다.
유니티 엔진은 비단 게임제작 뿐만 아니라 비게임분야(건축, 영화, 증강현실 등)에도 적용이 가능한 범용 엔진이기 때문에 프로그래밍 코드로도 모델링을 가능하게 하는 기능들도 기본적으로 포함되어 있습니다. 이번 포스팅에는 유니티엔진의 script를 이용하여 model의 기본요소들을 구성하는 내용을 다루겠습니다.
Modeling 구성요소
opengl 혹은 direct 계열의 rendering engine에서 사용 가능한 modeling file에는 수많은 구성요소가 존재합니다. 이를 모두 설명하는데는 한계가 있으므로 기본적인 모양을 만들 수 있는 구성요소만 다루도록 하겠습니다. 더불어 유니티의 C# script를 이용하여 유니티 상에서 구현하는 예제를 진행하겠습니다.
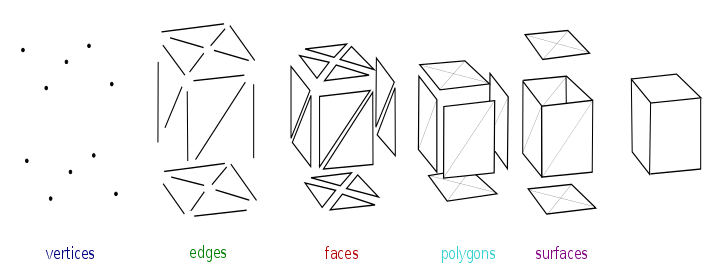
*Source: 위키백과
- Polygon
- 3D graphics의 기본 표현 단위
- 3차원 좌표를 가진 3개의 점으로 이루어진 구조체
- Edge: 두 점을 잇는 선
- Face: 세 점 이상을 이을때 생기는 폐곡면
- Mesh: model의 모양을 나타내는 edge 구조
- Mesh 구성요소
- vertex: 정점 위치정보
- triangles: polygon을 구성하는 vertex의 순서
- normal: face의 법선 vector
- uv: texture mapping을 위해 각 vertex가 가지고 있는 2차원 좌표(uvw라는 3차원 정보도 있으나 특수한 경우 아니면 2차원 uv만 사용)
- vertex color: 정점의 색정보(texture 없이 색을 표현하는 경우나 부가적인 표현을 위한 texture masking에 사용하기도 하나 일반적인 상황에서는 사용하지 않는다.)
Mesh 구성 예제(unity)
unity에서 mesh를 구성하기 앞서 숙지해야 할 부분은 vertex array와 triangles index의 순서에 따라 mesh 구성이 달라진다는 점입니다.
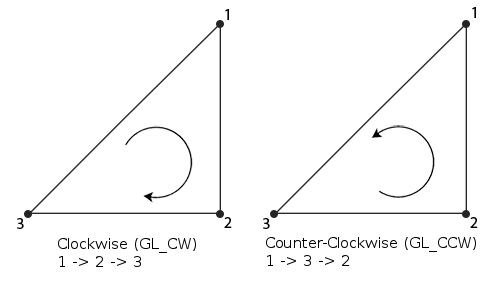*Source: opengl wiki
triangles index는 vertex array의 vertex index를 의미하는데, 이것의 배열 순서에 따라 면과 법선 방향이 결정됩니다.
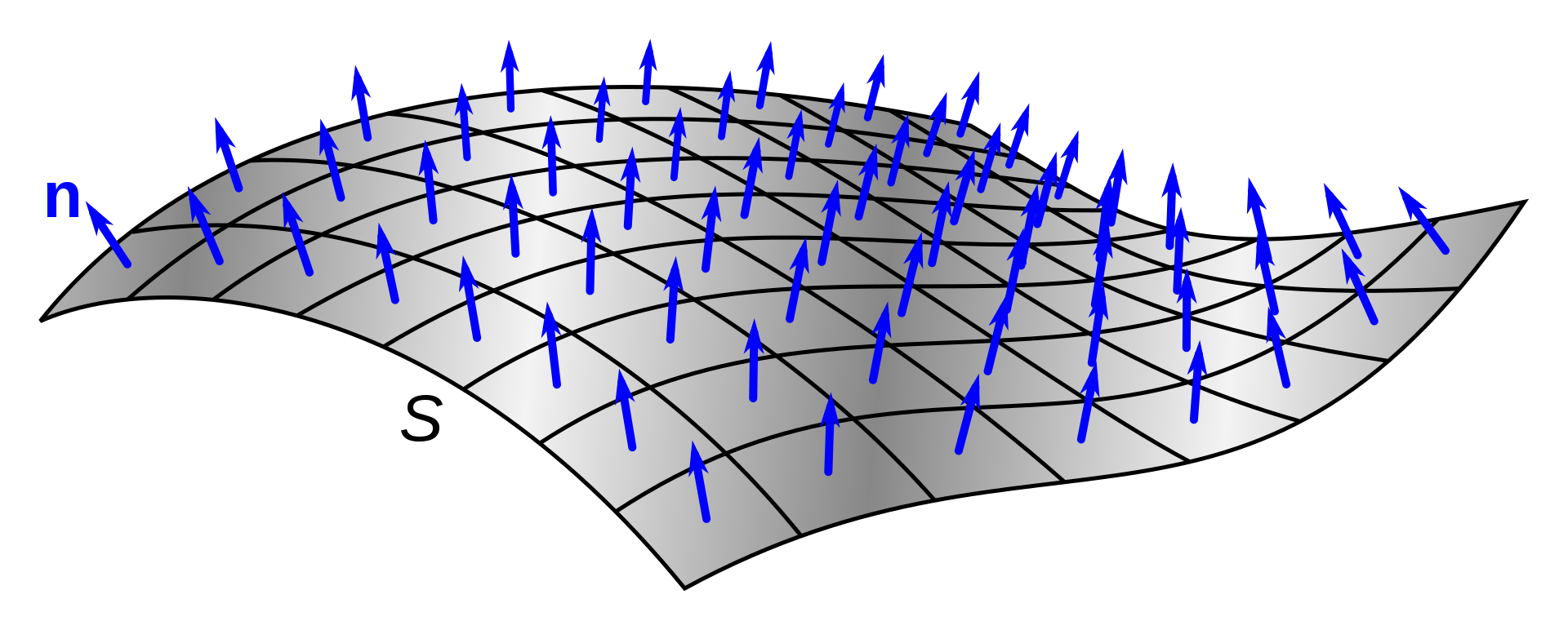
*Source: opengl wiki
법선은 면으로부터 수직 방향을 나타내는 방향입니다. triangles index의 배열 순서가 CW인지 CCW인지에 따라 법선의 방향이 결정되고, 이 법선벡터에 의해 랜더링할 면을 결정하게 됩니다. (일반적으로는 랜더링 부하 때문에 거의 드러나지 않는 면은 랜더링에서 제외하기 때문. Opengl 에서는 glFrontFace(GLenum mode)로 랜더링 방향을 결정. unity는 shader의 Cull로 결정)
polygon(triangle) 생성
이제 Unity에서 C# script를 이용한 기본 삼각형오브젝트를 제작해보겠습니다. (사용된 Unity version: 2018.3.0f2)
빈 gameobject에 PolygonMaker라는 script를 만든 후 component로 추가합니다.
그리고 PolygonMaker class에 단순한 삼각형 polygon을 만드는 다음 메소드를 만들어 줍니다.
public GameObject MakePolygon(Vector3 p1, Vector3 p2, Vector3 p3)
{
GameObject go = new GameObject("Poligon");
Mesh mesh = new Mesh();
MeshFilter mf = go.AddComponent<MeshFilter>();
MeshRenderer mr = go.AddComponent<MeshRenderer>();
Material mt = new Material(Shader.Find("Standard"));
Vector3[] vertices = { p1, p2, p3 };
Vector2[] uvs = { new Vector2(0, 0), new Vector2(1, 0), new Vector2(1, 1) };
int[] tris = { 0, 2, 1 };
mt.mainTexture = (Texture)Resources.Load("Texture/1941165_0");
mesh.vertices = vertices;
mesh.triangles = tris;
mesh.uv = uvs;
mf.mesh = mesh;
mr.material = mt;
return go;
}
다음과 같이, 세 점의 위치 vector를 parameter로 하는 polygon 제작함수를 만들었습니다. 주의할 점은, Unity의 standard shader default setting에서는 tris의 vertices index 월드좌표 기준으로 순서가 CW(clockwise)이면 랜더링 되는 면이 위를 향하고, CCW(counter clockwise)이면 아래를 향할 것입니다.
mesh의 uv는 쉽게 말하자면 model의 전개도로, x,y축으로 최대값 1을 갖고, uv의 index는 vertices의 index와 매칭됩니다. 즉, 해당 index의 버텍스의 uv좌표가 uv 배열의 해당 index를 가리킵니다. 만일 최대값 1을 넘길 시, texture는 반복적으로 나타나게 됩니다.
void Start()
{
MakePoligon(new Vector3(0, 0, 0), new Vector3(1, 0, 0), new Vector3(1, 0, 1));
}
그리고 제작한 메소드에 P1(0,0,0), P2(1,0,0), P3(1,0,1)의 세 점을 입력하여 폴리곤을 만듭니다.
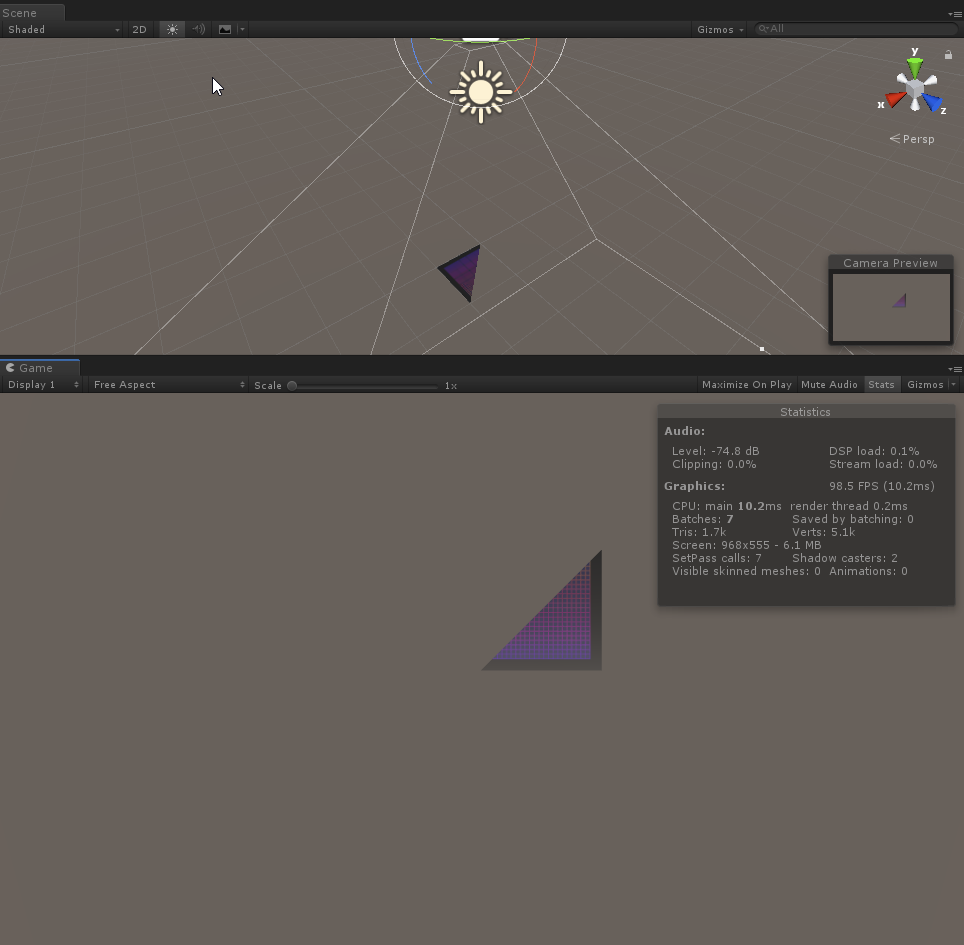
결과화면
위와 같이 월드좌표 기준 P1(0,0,0), P2(1,0,0), P3(1,0,1)을 꼭지점으로 하는 기본단위 폴리곤인 삼각형이 만들어진 것을 확인할 수 있습니다.
Unity에서 랜더링 할 수 있도록 GameObject를 만들고, MeshRenderer component와 MeshFilter component를 추가했으며, image를 불러서 입혀주는 일련의 과정을 모두 MakePolygon method 에서 수행하였습니다.
polygon(Quad) 생성
이번에는 동일한 방법으로 사각형 판(Quad) 오브젝트를 만들어 보겠습니다.
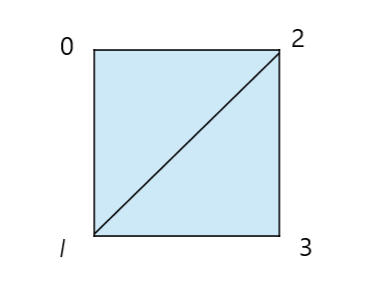
사각형을 만들때는 위와 같은 순서(예: 0,1,2,2,1,3)로 vertices index를 mesh의 triangles에 배치해야 합니다. 세개의 vertex를 triangles에 배치하고 나면, 자동으로 다음의 vertex 세개를 다른 triangle로 구분합니다. (사용된 Unity version : 2018.3.0f2)
public GameObject MakeQuad(Vector3 p1, Vector3 p2, Vector3 p3, Vector3 p4)
{
GameObject go = new GameObject("Quad");
Mesh mesh = new Mesh();
MeshFilter mf = go.AddComponent<MeshFilter>();
MeshRenderer mr = go.AddComponent<MeshRenderer>();
Material mt = new Material(Shader.Find("Standard"));
mt.mainTexture = (Texture)Resources.Load("Texture/corodinateChecker");
Vector3[] vertices = { p1, p2, p3, p4 };
Vector2[] uvs = { new Vector2(0, 0), new Vector2(1, 0), new Vector2(0, 1), new Vector2(1,1) };
int[] tris = { 0, 1, 2, 2, 1, 3 };
mesh.vertices = vertices;
mesh.triangles = tris;
mesh.uv = uvs;
mf.mesh = mesh;
mr.material = mt;
return go;
}
void Start()
{
MakeQuad(new Vector3(0, 0, 0), new Vector3(0, 0, 1), new Vector3(1, 0, 0), new Vector3(1, 0, 1));
}
mesh의 triangle index 순서에서 중요한 것은, 세 점이 삼각형을 이루는지와 점배치의 회전방향입니다. 시작점이 어떠한 것인지는 상관없습니다. 위 method에서 예를 들면 (0,1,2,2,1,3)의 순서 뿐만 아니라 (2,0,1,2,1,3), (2,0,1,3,2,1) 등의 순서도 가능합니다.
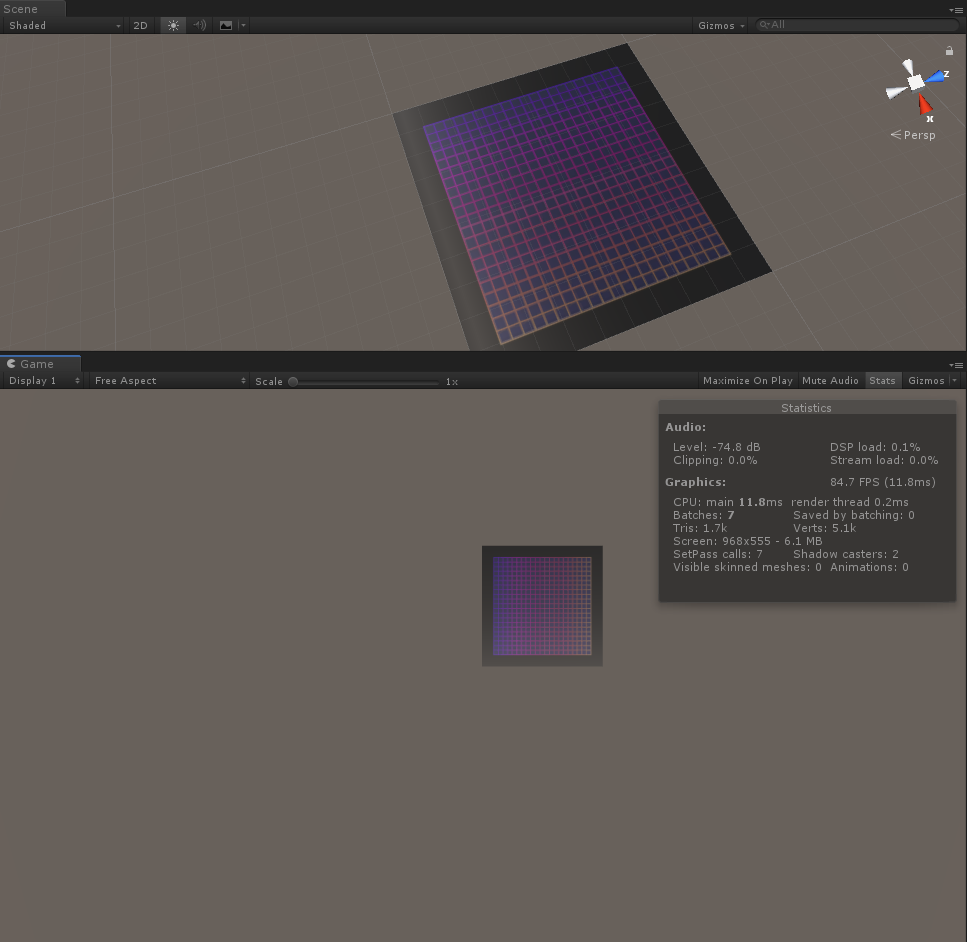
결과화면
polygon(Submesh quad) 생성
submesh란 하나의 geometry가 다수의 mesh로 이루어진 것을 말합니다. 이 구조는 각각의 mesh가 각기 다른 material 정보를 참조할 수 있기 때문에 하나의 오브젝트에서 여러 종류의 재질표현이 가능하지만, 하나의 오브젝트를 랜더링하기 위하여 여러 개의 material을 call 해야 하기때문에 랜더링 성능을 더 많이 소비합니다.
unity c# script에서도 submesh 생성이 다음과 같이 가능합니다. (사용된 Unity version : 2018.3.0f2)
public GameObject MakeSubmeshQuad(Vector3 p1, Vector3 p2, Vector3 p3, Vector3 p4, Vector3 p5, Vector3 p6)
{
GameObject go = new GameObject("subQuad");
Mesh mesh = new Mesh();
MeshFilter mf = go.AddComponent<MeshFilter>();
MeshRenderer mr = go.AddComponent<MeshRenderer>();
Material[] mts = new Material[2];
mts[0] = new Material(Shader.Find("Standard"));
mts[1] = new Material(Shader.Find("Standard"));
mts[0].mainTexture = (Texture)Resources.Load("Texture/corodinateChecker");
mts[1].mainTexture = (Texture)Resources.Load("Texture/corodinate");
Vector3[] vertices = { p1, p2, p3, p4, p5, p6 };
Vector2[] uvs = { new Vector2(0, 0), new Vector2(1, 0), new Vector2(0, 1), new Vector2(0, 1), new Vector2(1, 0), new Vector2(1, 1) };
int[] subTris1 = { 0, 2, 1 };
int[] subTris2 = { 4, 3, 5 };
mesh.vertices = vertices;
mesh.subMeshCount = 2;
mesh.SetTriangles(subTris1, 0);
mesh.SetTriangles(subTris2, 1);
mesh.uv = uvs;
mf.mesh = mesh;
mr.materials = mts;
return go;
}
submesh에서 특징적인 것은, 서로 다른 submesh들은 vertex를 공유하지 않는다는 겁니다. 그렇기 때문에 만일 4개의 꼭지점을 갖고 2개의 submesh를 갖는 geometry를 만들려면 총 6개(3 + 3)의 vertex가 필요합니다. 물론 꼭지점의 갯수는 4개이므로, 위치가 서로 겹치는 vertex들이 존재하게 됩니다.
상기 code에서 볼 수 있듯이, mesh의 SetTriangles method를 이용하여 나누고자 하는 vertices의 index를 나누어 각각의 subMesh들을 등록합니다. 첫번째 parameter는 triangle int 배열, 두번째 parameter는 subMesh의 index입니다. subMesh의 갯수는 subMeshCount 변수를 이용해서 선언합니다.
void Start()
{
MakeSubmeshQuad(new Vector3(0, 0, 0), new Vector3(1, 0, 0), new Vector3(0, 0, 1), new Vector3(0, 0, 1), new Vector3(1, 0, 0), new Vector3(1, 0, 1));
}
vertex가 6개인 quad(두개의 submesh triangle들이 하나의 quad를 이룬 경우)
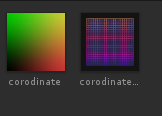MakeSubmeshQuad에서 각기 다른 texture와 material을 생성한 후, 적용한 결과
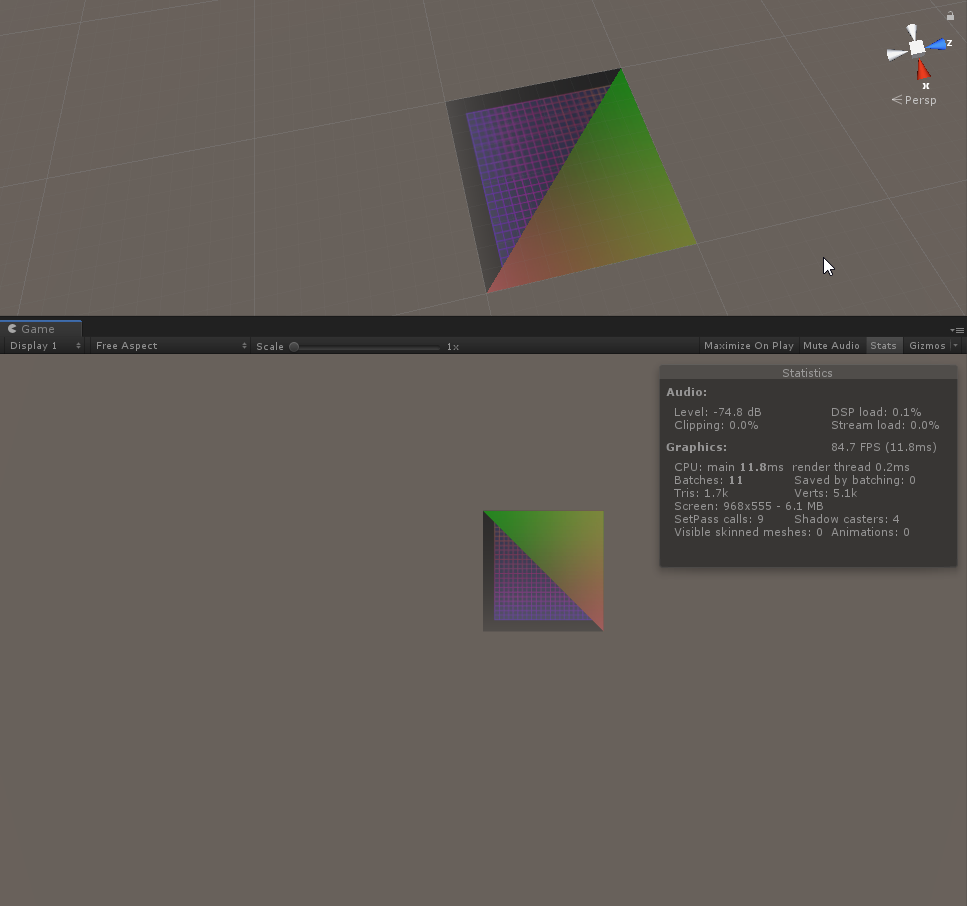각각의 submesh에 각기 다른 material이 적용되었음을 확인할 수 있습니다.
Transform matrix
Affine space & Affine transform
affine plane과 affine space는 유클리드 공간의 affine 기하학적 성질을 일반화해서 만들어지는 구조로, 점좌표에서 점좌표를 빼서 vector를 얻거나 점좌표에 vector를 더해 다른 점좌표를 얻을 수 있습니다. 이를 affine transform 이라고 부릅니다.
affine transform은 유클리드 3차원 공간에서 좌표의 이동, 스케일, 회전 등을 간단한 4X4 행렬식의 곱을 이용하여 변환하기 유용한 개념으로, vertex 및 오브젝트의 이동 등에 사용합니다. 라이브 스케치에서는 평면을 사출하여 체적을 만드는 알고리즘으로 벽 mesh를 생성하고 있습니다. 비단, object의 사출뿐만 아니라 변위가 생기는 모든 경우에 적용이 가능하므로 게임에서도 유용하게 사용됩니다.
하지만, Unity에서는 이런 affine transform 공식을 누구나 쉽게 쓸 수 있도록 Object 단위로 제어 가능한 transform method들을 쓰기 쉽게 만들어 놓았기 때문에 vertex 제어같은 드문 경우에서나 주로 사용합니다. 하지만 원리를 알아두면 예상치 못한 케이스들이나 native graphic framework들에 대한 대응도 가능하므로 개략적인 개념은 파악해두면 좋습니다.
우선 다항연립방정식을 효과적으로 처리할 수 있는 방식인 행렬연산을 이용하면 수월하게 계산 및 표기가 가능하기에(행렬연산이 발명된 이유이기도 하죠), 좌표관련 연산에는 행렬식이 무척 자주 쓰입니다.
3차원 유클리드 좌표계임을 가정했을때, x,y,z라는 세개의 parameter가 있고, 각 항에 곱해서 최종 아웃풋을 결정하는 비례계수가 존재합니다. 각 output X,Y,Z에는 input x성분, y성분, z성분의 합으로 나타나는데, 이것은 각 최종 좌표가 세가지 input parameter에 유기적으로 변하기 때문입니다. 예를 들어, 간단한 2차원 원방정식만 해도 각각의 x, y항을 구하기 위해서는 x와 y간의 연산을 필요로 합니다.
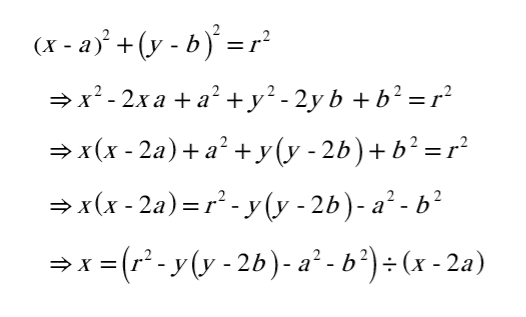물론 연산된 식은 상당히 복잡하게 상수와 변수가 혼재되어 있으나 좌항과 우항이 homogeneous(동차적) 형태이므로, 비례계수를 변수에 곱해주는 식으로 변형이 가능해집니다.
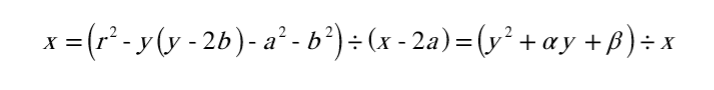(여기서 2차원 원방정식의 예시는 왜 항을 구할때 각 항의 덧셈과 같은 구조가 되는지와 동차적 구조에 대한 설명을 위한 것으로 affine transform에서는 동차가 아니기 때문에 원방정식을 쓰지는 않습니다. 그래서 affine 변환에서의 회전은 차원 형태를 맞추기 위해서 삼각함수를 이용합니다. 이 방법에 대해서는 뒤에 회전변환때 설명하겠습니다.)
유클리드 공간의 vector를 나타낸 비례상수와 x,y,z parameter의 곱과 합을 다음과 같은 행렬식으로 전환할 수 있습니다.
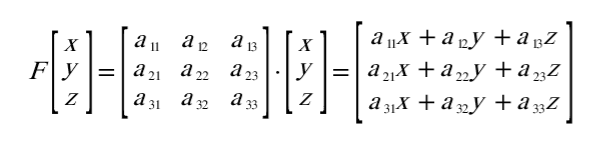
하지만 이 식에서는 방향성분만 존재합니다. 방향을 이동한다는 것은 불가능하므로, 위치에 대한 정보도 필요합니다. 그러므로 3차원 공간에 대한 위치행렬 t를 더해보면 다음과 같은 형태가 됩니다.
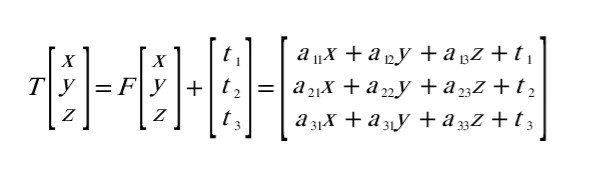
이 행렬의 덧셈을 정사각 행렬로 하나로 묶어주는 것도 가능합니다. 그렇게 하기 위해서는 가상의 차원을 하나 더 늘립니다.
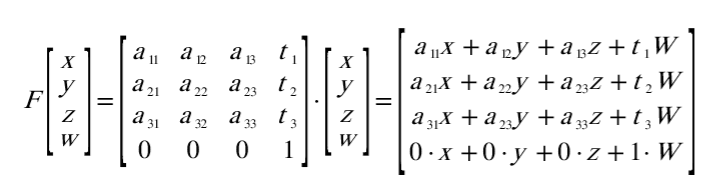
이런 4차원 형태로 만드는 이유는, 이동, 회전, 확대 변환행렬들의 곱을 더 쉽게 할 수 있는 형태로 만들고, 또 transform의 방향성(w)도 지정할 수 있기 때문입니다.
이제 행렬을 이용한 affine 공간에서의 회전에 대해 설명하겠습니다.
2차원에서의 회전행렬은 다음과 같은 식으로 나타납니다.
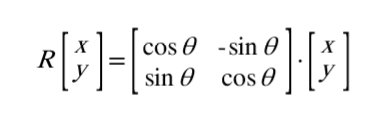
이를 증명하기 위해서는 간단한(?) 삼각형의 정의와 선형수학만 있으면 됩니다.
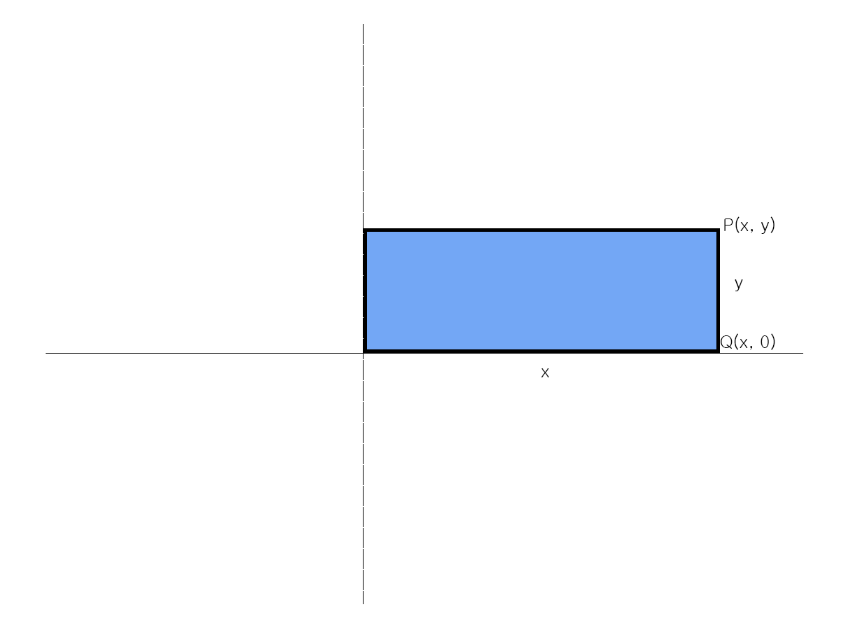
다음과 같은 직사각형이 존재한다고 하고, 우측의 두 점을 길이가 각각 x, y인 P, Q 라고 정의합니다.
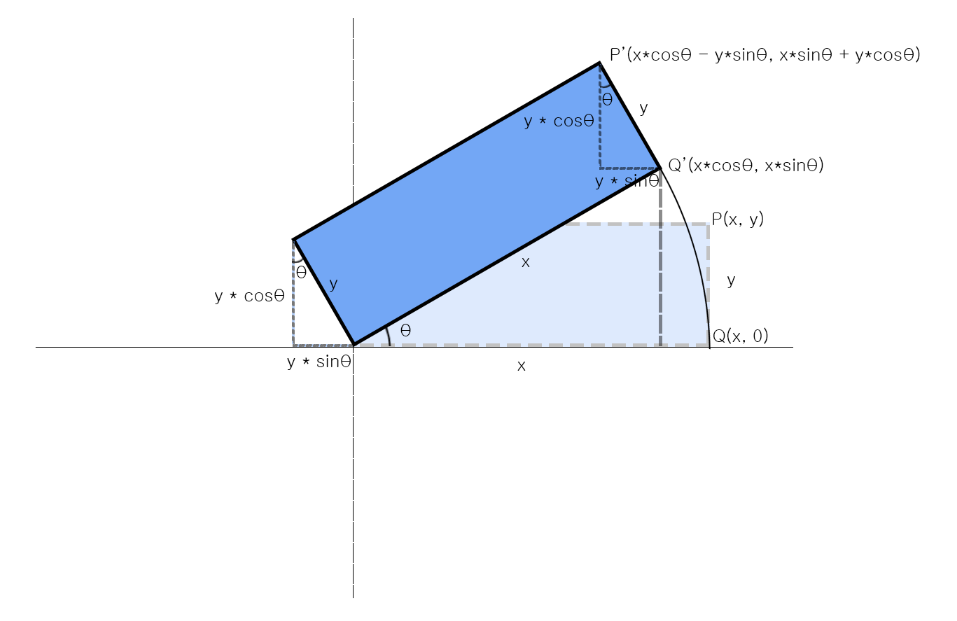
이 직사각형을 euler 각도 θ만큼 회전하였을때 P, Q의 위치를 P’, Q’라고 하면, 이 P’, Q’의 좌표는 P’(xcosθ - ysinθ, xsinθ + ycosθ), Q’(xcosθ, xsinθ)가 됩니다. 쓰인 개념은 피타고라스의 정리와 삼각함수의 정의, 삼각형의 정의 뿐이고, 도식으로도 충분히 이해가 가능합니다.
행렬의 성질에 의해 다음과 같이 회전행렬을 적용할 수 있고,
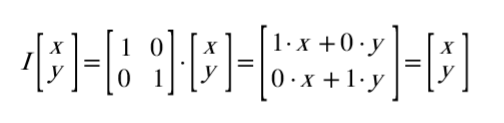
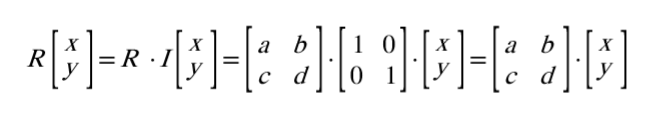
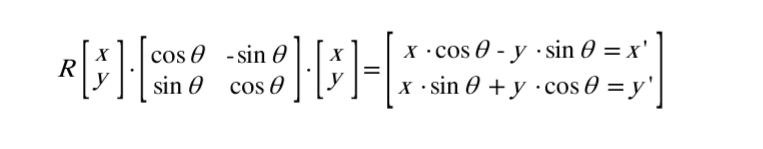
도출된 식의 P(x, y)를 P’(xcosθ - ysinθ, xsinθ + ycosθ)의 형태로 나오게 분해해보면 다음과 같은 회전행렬식을 도출할 수 있습니다. 또한 각 축에 대해 회전변환 행렬을 순차적으로 곱해주면 순서대로 회전시킨 최종 결과를 얻을 수 있습니다.
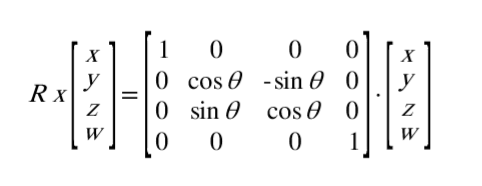
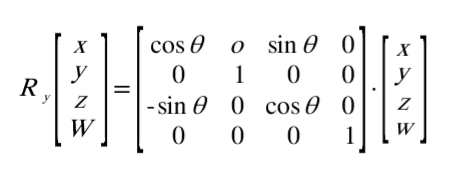
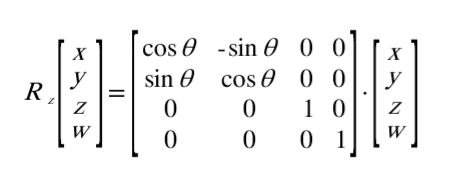
2차원 상에서의 회전행렬이지만 3차원은 결국 xy평면, yz평면, xz평면에서 회전을 하면 2차원과 같은 구조이므로, 다음과 같은 유사한 형태의 식을 도출할 수 있습니다. (3차원 회전식의 경우에는 원리는 같지만 복잡성이 늘어나므로, 증명과정의 기술은 생략하도록 하겠습니다. 더 자세한 설명은 선형대수학을 참고하시면 됩니다.)
affine 공간에서의 scale 식은 간단합니다. 행렬의 분배법칙에 의해서 단위행렬 I에 scale factor를 더해준 형태가 scale 식이기 때문에 다음과 같은 형태가 됩니다.
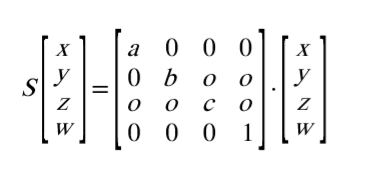
이렇게 구한 transform, rotation, scale 행렬을 서로 곱해주면, affine 공간에서 이동, 회전, scale이 적용된 최종 아웃풋을 얻을 수가 있습니다. 단, 행렬의 특징중, 교환법칙은 성립되지 않기 때문에, 반드시 transform, rotation, scale 순으로 각 행렬들을 곱해줘야 제대로 된 결과를 얻을 수 있습니다.
TRS test code
여지껏 수학적 증명을 하면서 trs 행렬과 변환을 설명한 이유는, unity의 3D 공간이 affine space이기 때문입니다. 하지만 unity를 하면서 이러한 행렬연산을 접하지 않으신 분들은 의아해 하실수도 있습니다. 사실은 unity에서 제공하는 transform class의 method들이 이런 행렬식을 이용해 만들어진 method들이지만, 패킹되어있기 때문에 내용 확인은 어렵습니다.
하지만 이러한 transform class는 gameObject 기준으로 사용에 제한이 있기 때문에 vertex 제어에는 불편함이 따릅니다. 그래서 vertex의 trs변환을 위해서 이러한 matrix 곱을 사용하는게 좋습니다. 이러한 경우를 상정했던 것인지, UnityEngine namespace의 Matrix4x4 class에서는 affine space에 적용 가능한 행렬곱 method들이 잘 준비되어 있습니다. 그러므로 unity에서 행렬곱까지 직접 구현할 필요는 없으나, 원리와 구조를 알아야 이 method들을 적재적소에 활용 가능합니다.
vector translate
위에서 설명한 이동행렬을 code로 쓰면 다음과 같습니다.
//vector의 이동
public static Matrix4x4 Translate(Vector3 aPosition)
{
var m = Matrix4x4.identity; // 1 0 0 x
m.m03 = aPosition.x; // 0 1 0 y
m.m13 = aPosition.y; // 0 0 1 z
m.m23 = aPosition.z; // 0 0 0 1
return m;
}
vector rotation
회전 같은 경우는 x, y, z축을 각각 회전시켜서 나온 행렬을 순서대로 곱해주면 x, y, z축 모든 방향으로 돌린 결과가 나옵니다.
//vector의 회전
public static Matrix4x4 RotateX(float aAngleRad)
{
Matrix4x4 m = Matrix4x4.identity; // 1 0 0 0
m.m11 = m.m22 = Mathf.Cos(aAngleRad); // 0 cos -sin 0
m.m21 = Mathf.Sin(aAngleRad); // 0 sin cos 0
m.m12 = -m.m21; // 0 0 0 1
return m;
}
public static Matrix4x4 RotateY(float aAngleRad)
{
Matrix4x4 m = Matrix4x4.identity; // cos 0 sin 0
m.m00 = m.m22 = Mathf.Cos(aAngleRad); // 0 1 0 0
m.m02 = Mathf.Sin(aAngleRad); //-sin 0 cos 0
m.m20 = -m.m02; // 0 0 0 1
return m;
}
public static Matrix4x4 RotateZ(float aAngleRad)
{
Matrix4x4 m = Matrix4x4.identity; // cos -sin 0 0
m.m00 = m.m11 = Mathf.Cos(aAngleRad); // sin cos 0 0
m.m10 = Mathf.Sin(aAngleRad); // 0 0 1 0
m.m01 = -m.m10; // 0 0 0 1
return m;
}
//최종 회전 결과
public static Matrix4x4 Rotate(Vector3 aEulerAngles)
{
var rad = aEulerAngles * Mathf.Deg2Rad;
return RotateY(rad.y) * RotateX(rad.x) * RotateZ(rad.z);
}
vector scale (world coordinate)
scale은 간단한 형태로 다음과 같습니다.
//vector의 확대/축소
public static Matrix4x4 Scale(Vector3 aScale)
{
var m = Matrix4x4.identity; // sx 0 0 0
m.m00 = aScale.x; // 0 sy 0 0
m.m11 = aScale.y; // 0 0 sz 0
m.m22 = aScale.z; // 0 0 0 1
return m;
}
TRS Test
앞서 생성했던 quad mesh를 이용하여 간단한 TRS Test를 해보겠습니다.
public class PolygonMaker : MonoBehaviour
{
// Start is called before the first frame update
void Start()
{
//quad object size
const float width = 1;
const float height = 1;
//gameObject 생성
Mesh mesh = MakeQuad(new Vector3(-width/2, 0, -height/2), new Vector3(-width/2, 0, height/2), new Vector3(width/2, 0, -height/2), new Vector3(width/2, 0, height/2)).GetComponent<MeshFilter>().mesh; 1)).GetComponent<MeshFilter>().mesh;
GameObject go = new GameObject("extruded Mesh");
Material mt = new Material(Shader.Find("Standard"));
go.AddComponent<MeshFilter>();
go.AddComponent<MeshRenderer>().material = mt;
//변환값을 저장할 새로운 위치 리스트
List<Vector3> newVert = new List<Vector3>();
//mesh의 vertices의 갯수 만큼 반복
foreach (Vector3 v in mesh.vertices)
{
Matrix4x4 fx;
Matrix4x4 fxT;
Matrix4x4 fxR;
Matrix4x4 fxS;
//변환행렬곱 수행
fxT = Translate(new Vector3(2f, 0f, 0f));
fxR = Rotate(new Vector3(45f, 0f, 0f));
fxS = Scale(new Vector3(0.5f, 2f, 2f));
//변환행렬 합성 (x축으로 2만큼 평행이동, x축기준 45도 회전, x축기준 0.5배 scale)
fx = fxT * fxR * fxS;
newVert.Add(fx.MultiplyPoint(v));
}
//mesh의 위치정보 갱신
mesh.vertices = newVert.ToArray();
}
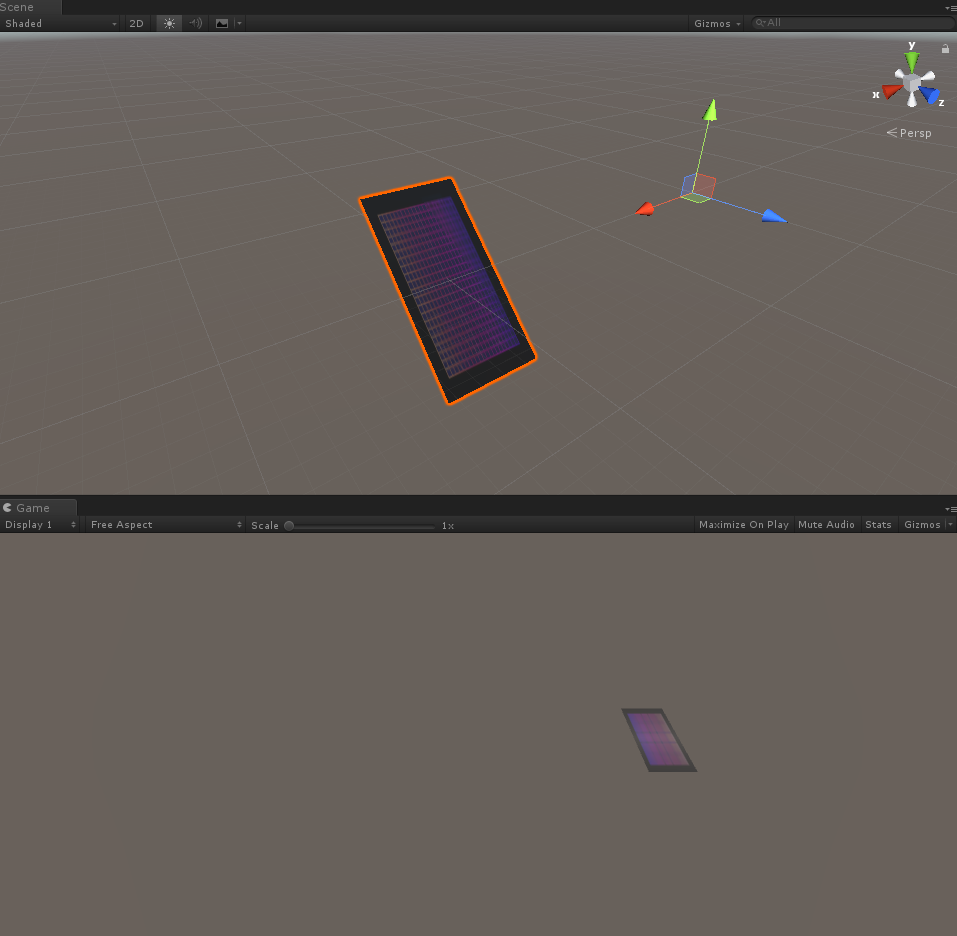결과화면
object의 pivot은 유지한채로 geometry만 변화시키므로, pivot을 다시 설정하는 상황에 써도 적합합니다.
맺음말
간단한 형태의 mesh 동적 생성과 affine space와 TRS 변환에 대해 알아보았습니다.
절차지향 모델링은 깊은 수학적 지식과 논리력을 필요로 합니다. (우리가 당연하게 생각했던 3ds max나 maya, blender같은 modeling tool들은 사실은 수학 및 논리적 algorithm의 집합체입니다.)
원리에 대한 이해가 없이 라이브러리나 다른 사람들이 만들어 놓은 api를 사용한다면 당장은 쉽게 갈 수 있을지 모르나, 결국 문제가 발생하면 한계에 봉착하고 다시 되돌아가서 생각하게 됩니다. 포스팅을 진행하면서 저 또한 스스로 더 노력해야 한다는 마음가짐을 갖게 되었습니다.
더 많은 내용을 쓰고 싶은 욕심도 있었으나 하다보니 분량이 늘어나서.. 더 깊은 내용은 다음 기회에 포스팅 하도록 하겠습니다. 감사합니다.
Subscribe via RSS